[CSS3] matrix3d 與 rotate3d 之到底在轉什麼鬼

剛泡好咖啡。對著電腦，路上無車無人，夜深無聲。沉默太久，傷害也太重，我想該是和大家清楚說幾句話的時候。前些日子，收到吳姓網友的訊息，說有一些問題想要討論一下，就此展開了一個奇幻旅程。

近期因為 VR 的產品像是雨後春筍般的冒出來，相關的應用也慢慢的在發展當中，例如 Youtube 加上 Google Cardboard 的應用，諸如此類的東西，貌似變成了一種潮流。

3D 列印

Image source: http://heckifiknowcomics.com/post/134582065049

其實在 stackoverflow 就有類似解答，

http://stackoverflow.com/questions/29716215/using-device-orientation-with-3d-transforms

收工啦（欸

matrix3d

吳姓網友的問題，是想在瀏覽器中，製作一個可以依照行動裝置陀螺儀資訊，相對旋轉的物體。根據 w3c 所說，陀螺儀所傳出來的資訊，我們可以透過 DeviceMotionEvent 來拿到，會有三個數字，依照 html5rocks 的說明，三個數值分別是：

gamma，對於 Y 軸旋轉的角度變化
beta，對於 Z 軸旋轉的角度變化
alpha，對於 X 軸旋轉的角度變化

所以，我們就很開心的想說，利用 matrix3d 來去旋轉一個 3D 立方體，用來達到手機旋轉，立方體跟隨的一個動作。

但是！~~事情不是憨人想的那麼簡單！~~

我們馬上遇到 matrix3d 在旋轉上面的一些特性，具體的結果實在沒有辦法用文字描述，這裡有一個網站，有興趣的人，可以依照我說的步驟試試看，

開啟 3D MODE
X 的 ROTATE 輸入 170
X 的 ROTATE 輸入 180
X 的 ROTATE 輸入 190
X 的 ROTATE 輸入 0
Y 的 ROTATE 輸入 170
Y 的 ROTATE 輸入 180
Y 的 ROTATE 輸入 0
Z 的 ROTATE 輸入 170
Z 的 ROTATE 輸入 180

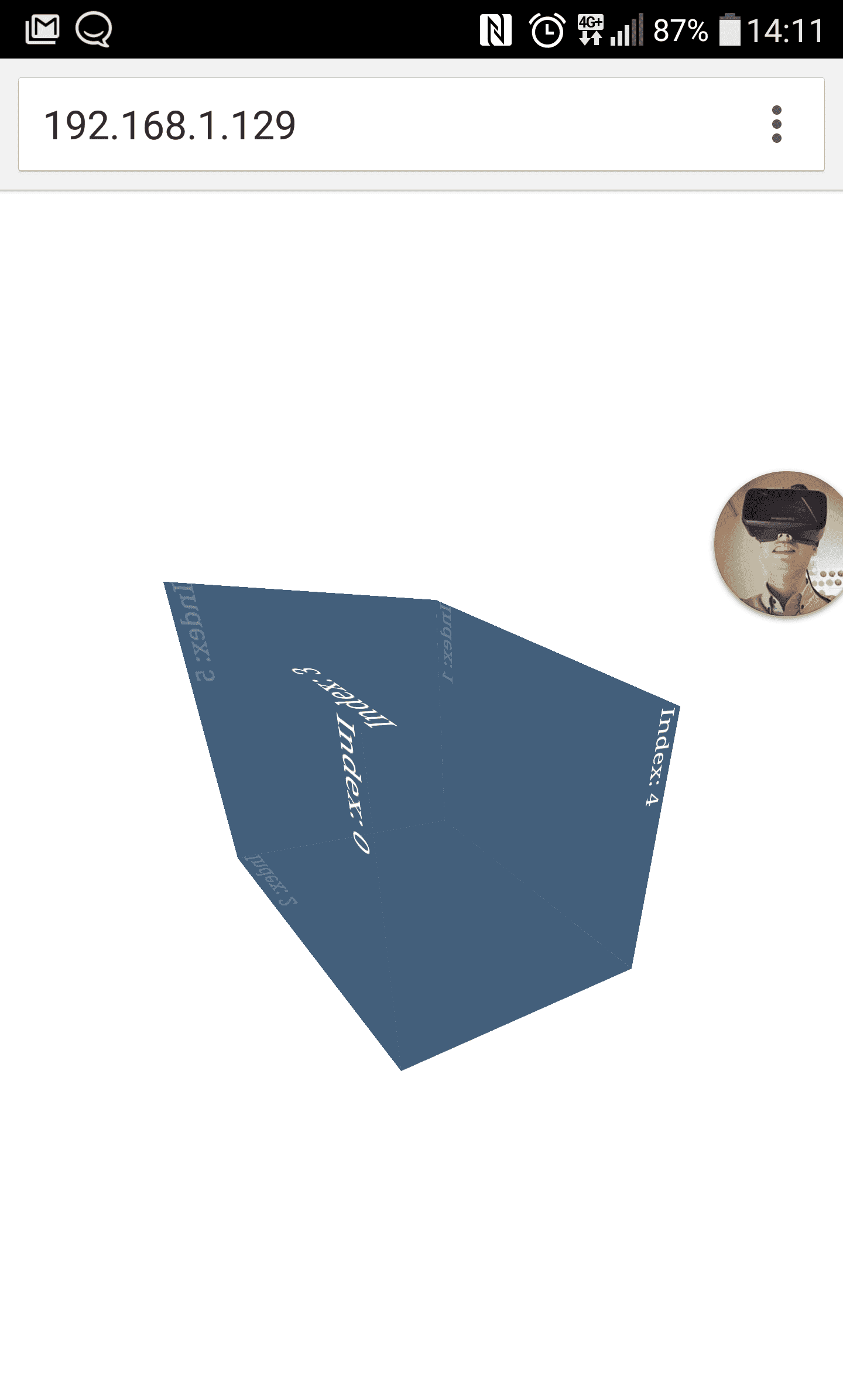
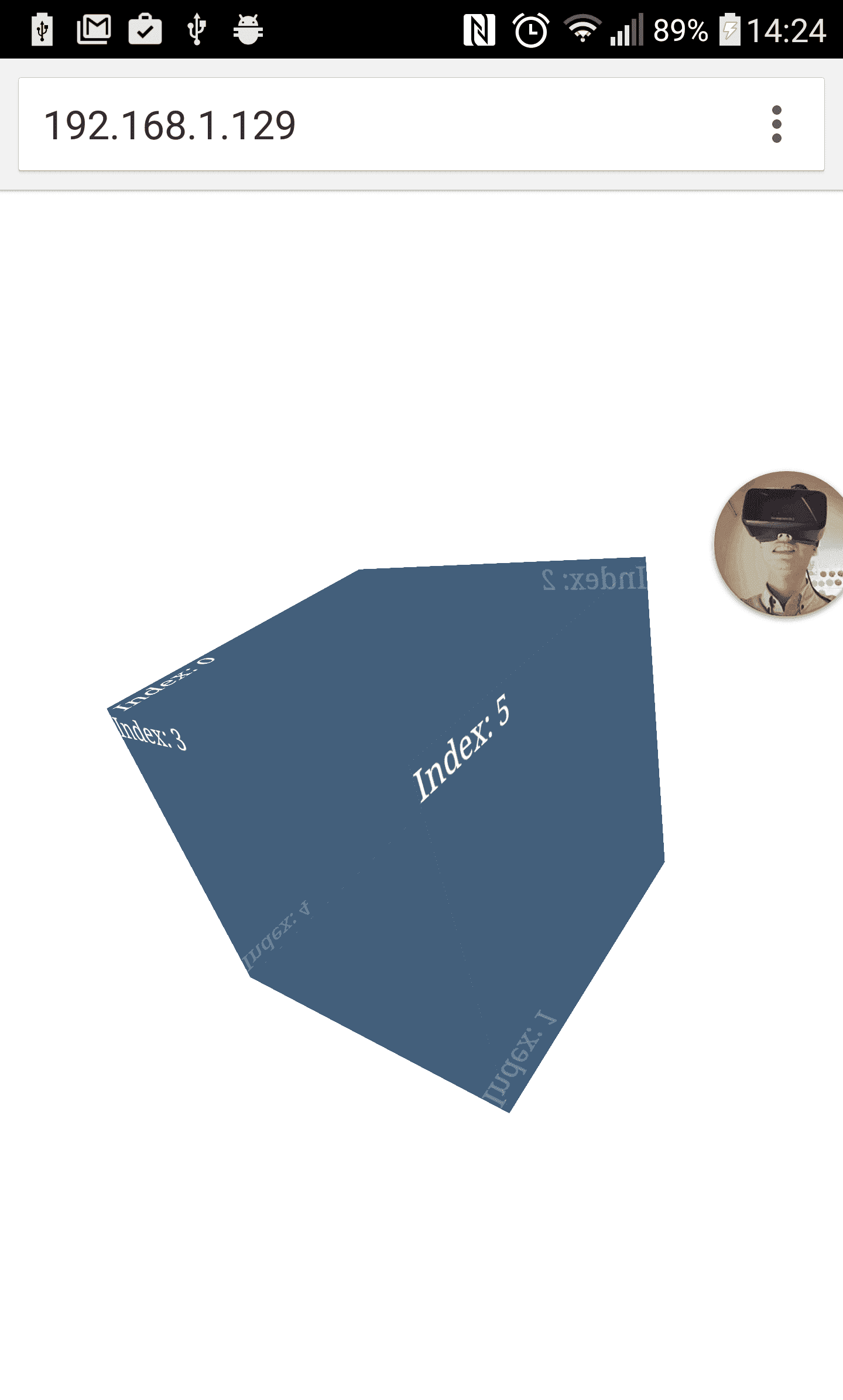
你會發現，上面那張圖片貌似先翻了 180 度之後，再轉去你要的 190 這個角度（對 X 軸來說）。這是我們遇到的第一個問題，也是唯一的問題，接近任何一個軸旋轉的極限值之後，會發生翻轉。這種翻轉事件在 3D 正方體的視角中，你會完全看不到背面。

意思就是，當 X 軸翻轉到極限值 180，他只會將正方體翻面，然後用翻面後的向量轉成 190 給你看。至於什麼是翻面後的向量，具體可以參考這裡對於旋轉的矩陣方程式：

https://en.wikipedia.org/wiki/Rotation_matrix

之後我不死心去翻了 w3c 關於這方面的解釋，其中寫到，

http://www.w3.org/TR/css-transforms-1/#mathematical-description

A 3D rotation with the vector $[x, y, z]$ and the parameter $\alpha$ is equivalent to the matrix:

$$
\begin{pmatrix}
1 - 2 * (y^2+z^2) * sq & 2 * (x * y * sq - z * sc) & 2 * (x * z * sq + y * sc) & 0\\
2 * (x * y * sq + z * sc) & 1 - 2 * (x^2+z^2) * sq & 2 * (y * z * sq + x * sc) & 0\\
2 * (x * z * sq - y * sc) & 2 * (y * z * sq + x * sc) & 1 - 2 * (x^2+y^2) * sq & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
$$

其中 sq, sc 分別是，

$
sc = sin(\alpha / 2) * cos(\alpha / 2)\\
sq = sin^2(\alpha / 2)
$

這個矩陣是針對某一個向量座標軸 $[x, y, z]$ 來旋轉一個 $\alpha$ 的角度。然後，結果不是我們想要的，旋轉超越極限值之後，就開始出現奇怪的變形透視。

Matrix3D Rotate

後來不死心再去研究一下 DeviceMotionEvent 所輸出的數字，實際上發現，那三個數值確實是 $[x, y, z]$ 三軸變化沒有錯，但是，沒有告訴你的是，這三個角度改變的不只是角度，而是座標向量轉變所衍生出來的。詳細解釋可以看看這個，

https://en.wikipedia.org/wiki/Euler_angles

一圖解千言，

Euler angles

By Lionel Brits (Hand drawn in Inkscape by me) [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons

所以，當作標系角度轉換了，我們要旋轉的東西，就不是單純的 $[\alpha, \beta, \gamma]$ 可以解決的事情了。

rotate3d

所以我把目標放到 rotate3d 上面。

Rotate3d

研究過程中發現了這個，

http://www.w3.org/Talks/2012/0416-CSS-WWW2012/Demos/transforms/demo-rotate3d.html

Watch out! vertical Y axis in 3d is inverted.

這就是為什麼我們直接將 $[\alpha, \beta, \gamma]$ 拿來用會出現的問題。所以，依照 rotate3d 的設定，每次旋轉必須要重新定義座標軸的向量，再來旋轉相對應的角度，就能避開這些狀況。

對於 3D 座標軸的轉換，可以用 wiki 提供的公式來解，

$$
\begin{pmatrix}
cos\theta + v_x^2 * (1 - cos\theta) & v_x * v_y * (1 - cos\theta) - v_z * sin\theta & v_x * v_z * (1 - cos\theta) + v_y * sin\theta\\
v_y * v_x * (1 - cos\theta) + v_z * sin\theta & cos\theta + v_y^2 * (1 - cos\theta) & v_y * v_z * (1 - cos\theta) - v_x * sin\theta\\
v_z * v_x * (1 - cos\theta) - v_y * sin\theta & v_z * v_x * (1 - cos\theta) + v_x * sin\theta & cos\theta + v_z^2 * (1 - cos\theta)
\end{pmatrix}
$$

接著要操作座標軸轉換，根據 w3c 表示，三個數值的邊界值分別是：

$\alpha = [0, 360]$
$\beta = [-180, 180]$
$\gamma = [-90, 90]$

再根據 Euler Angles 來做一次座標轉換，

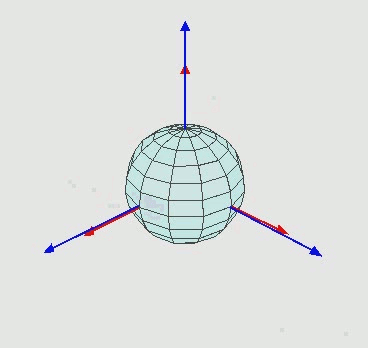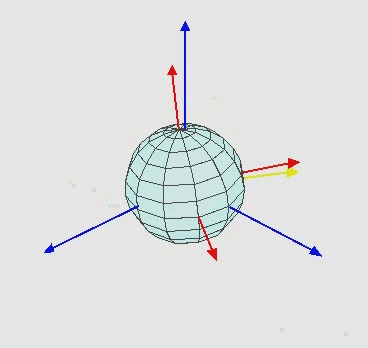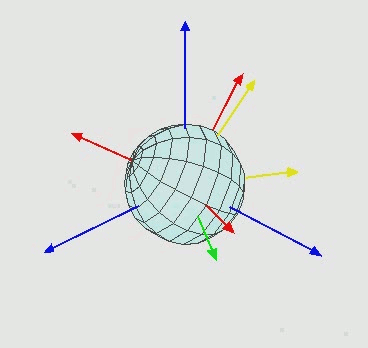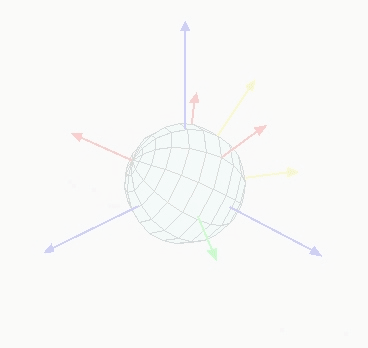
By Euler2.gif: Juansempere derivative work: Xavax (This file was derived from Euler2.gif:) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons

程式碼

// https://en.wikipedia.org/wiki/Rotation_matrix
// 向量座標軸轉換
function rotateMatrix(axis, angle) {
  var sc = Math.cos(angle * Math.PI / 180.0),
      sq = Math.sin(angle * Math.PI / 180.0),
      x = axis[0],
      y = axis[1],
      z = axis[2];

  var rm = [
    [0,0,0],
    [0,0,0],
    [0,0,0],
  ];

  rm[0][0] = sc + x*x * (1-sc);
  rm[1][0] = z*sq + y*x * (1-sc);
  rm[2][0] = -y*sq + z*x * (1-sc);
  rm[0][1] = -z*sq + x*y * (1-sc);
  rm[1][1] = sc + y*y * (1-sc);
  rm[2][1] = x*sq + z*y * (1-sc);
  rm[0][2] = y*sq + x*z * (1-sc);
  rm[1][2] = -x*sq + y*z * (1-sc);
  rm[2][2] = sc + z*z * (1-sc);

  return [
    rm[0][0] * vector[0] + rm[0][1] * vector[1] + rm[0][2] * vector[2],
    rm[1][0] * vector[0] + rm[1][1] * vector[1] + rm[1][2] * vector[2],
    rm[2][0] * vector[0] + rm[2][1] * vector[1] + rm[2][2] * vector[2]
  ];
}

// 預設座標軸向量
var default_vector = {
  x: [1, 0, 0],
  y: [0, 1, 0],
  z: [0, 0, 1],
};

window.ondeviceorientation = function(event) {
  var alpha = Math.floor(event.alpha),
      beta = Math.floor(event.beta),
      gamma = Math.floor(event.gamma) * -1;

  // 轉換座標軸向量
  var axis = { x:0, y: 0, z: 0 };
  // 用上面那個 GIF 圖片的順序來做轉換
  axis.y = default_vecotr.y;
  axis.x = rotateMatrix(default_vector.x, axis.y, gamma);
  axis.z = rotateMatrix(rotateMatrix(default_vector.z, axis.y, gamma), axis.x, beta);

  // 最後使用 rotate3d 寫入 transform
  // 要注意的是，三軸順序是 Z -> X -> Y
  // 等於將上面那張 GIF 圖片順序倒過來放
  document.getElementById('#box').style.transform = 'rotate3d(' + axis.z[0] + ', ' + axis.z[1] + ', ' + axis.z[2] + ', ' + alpha + 'deg) ' + 'rotate3d(' + axis.x[0] + ', ' + axis.x[1] + ', ' + axis.x[2] + ', ' + beta + 'deg) ' + 'rotate3d(' + axis.y[0] + ', ' + axis.y[1] + ', ' + axis.y[2] + ', ' + gamma + 'deg)';
};

實際展示，請用手機開啟 http://jquery.hinablue.me/cube.html

跑起來好像頗正常，不過好像在不同裝置上會有意想不到的錯誤。你可以拿著手機旋轉、跳躍~~，我閉上眼。~~

就，再研究了。

後記

也許你會問，為什麼要從 Y 軸開始？好問題，因為我試過其他兩軸，無論你向量再怎麼正確，rotate3d 出來就是很詭異，整個方塊的動作跟手機的操作是違合的，具體是什麼原因我不太清楚。要搞清楚可能得去找數學系的吧（哈哈哈

~~感恩吳姓網友，雷射吳姓網友。~~

matrix3d

rotate3d

程式碼

後記

You might also like...