r2 = b2 + (r-a)2
r2 = b2 + r2 -2ar+r2
r = b2/ 2a
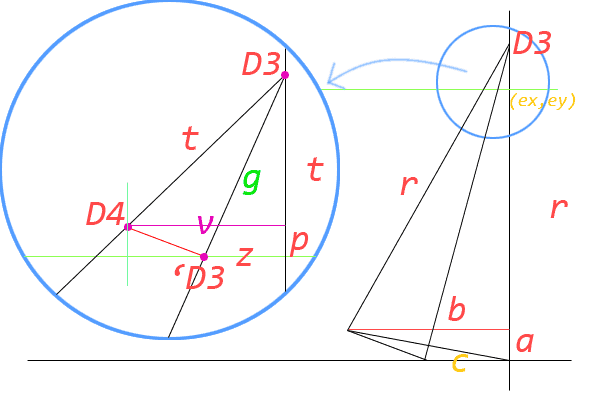
求得第三點 D3 的座標值 (ex, r),上圖綠色的線代表書本上緣的邊界值,所以 r 值其實已經超出了邊界值(r > ey),所以必須要再次計算翻頁出來的真正 D3 的位置。由直角三角形比例線段求得點 D3 對於邊界值的距離 z。
r/c = t/z
z = tc / r
所以新的 D3 座標值應該為 (ex - z, ey),其中 z 為 (r - ey)*c / r,求得新的 D3 座標點後,接下來要求的是 D4 的座標點。
(v - z)2 + p2 = z2 -> p2 = z2 - (v - z)2
v2 + (t - p)2 = t2
v2+ t2- 2pt + p2= t2
v2+ t2- 2pt + (z2- (v - z)2) + p2= t2
v = pt / z
p2 = z2 - (v - z)2
p2 = 2(pt/z)z - (pt/z)2
pz2 = 2tz2 - pt2
p = 2tz2/ (z2+ t2)
p = 2tz2/ g2
v = (2tz2/ g2)(t/z)
v = 2t2 z / g2
已上求得點 p, v 對於上緣極限值的距離,所以可得點 D4 的真實座標值為 ( ex - v, ey - p )。倘若點 D3 沒有超出上緣極限值,則 D3 = D4 為共點。
基本上,若是以矩形對角線相交點為二元座標原點,則書本四個角落分別就是四個象限,公式都一樣,只有正負值的變化而以。

