[AS3 note.] 翻頁座標分析 part 1

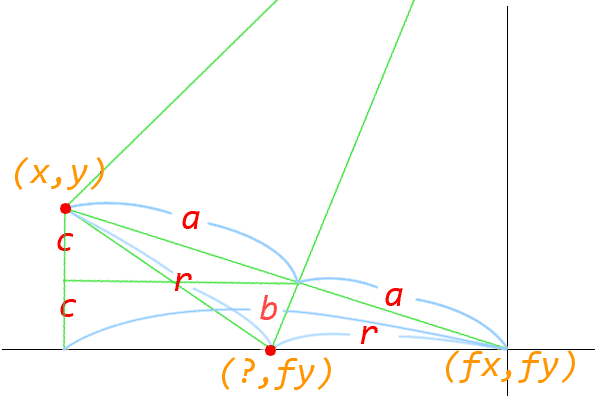
r² = (2c)² + (b-r)²

r² = 4c² + b² -2br+r²
r = 4c²/2b + b/2
r = ((2a)² -b² )/2b + b/2
r = 2a²/ b

故在滑鼠任意點 (x,y) 與已知點 (fx,fy) 可求得底邊點 (r, fy)。則 r 點 x 座標值為 fx - 2a²/ b，其中：

a = 1/2 ( sqrt((fy-y)² + (fx-x)² )

b = fx-x

所以，就這樣