矩陣的乘法就不贅述了,對了,我除了英文不好以外,數學也特爛。這六個數字分別代表的意義,可以在英文詳解的 Other Interesting Facts About Matrices 中看出端倪。
這樣看得出端倪嗎?所有的 CSS3 變形效果,都可以用 Matrix 來做到,而實際上,瀏覽器似乎也是把所有的效果全部轉換為 matrix 去執行(只是我們並不知道而已)。這麼看來,我們可以小結一下:
- 1, 4 是縮放變形的結果
- 5, 6 是位移變形的結果
- 2, 3 是歪斜變形的結果
- 1, 2, 3, 4 是旋轉變形的結果
所以,其實 matrix 是一個因,而瀏覽器執行這個設定所顯示出來的是果。讓開發出現難度的地方是,你無法精準控制所產生的結果是否如預期。而,上述的英文詳解網站也有做一個讓你 實踐操作的工具頁面,你可以去這裡把玩看看,建議使用 Chrome 或是 Firefox 啦,IE 不能動,還有什麼值得我心痛(許茹雲,淚海
所以,我該怎麼去推測結果?首先,我先假設一個方塊,將變形的原點(transform-origin)設定為 (0,0),是的,如果變形的原點不同,所產生的結果也是不一樣的。那麼,我現在有一個 100x100 的矩陣,然後我要作一個變形,我們隨意取一個值來測試:
-moz-transform: matrix(0.6924, 1.2, -0.3216, 1.2, 50px, 100px);
-webkit-transform: matrix(0.6924, 1.2, -0.3216, 1.2, 50, 100);
-o-transform: matrix(0.6924, 1.2, -0.3216, 1.2, 50, 100);
transform: matrix(0.6924, 1.2, -0.3216, 1.2, 50, 100);
如果把這些數字換成矩陣,那就會長這個樣子:
我們的方塊有四個角落,所以就分別有四個座標值,因為是二元的,所以作成 3x1 的矩陣就是:
然後我們來作矩陣的相乘,由於我數學太爛,所以我取 100 只是剛好而已:
所以這樣我們就有新的座標點了:
A' (50, 100)
B' (119.24, 220)
C' (18.84, 220)
D' (87.08, 340)
用新的座標點所畫出來的圖形(因為我們的 transform-origin 設定為 (0,0) 所以不影響變形座標軸),就是做完變形之後的圖形。在 matrix 中的前四個數字,由於是從 skew,rotate 與 scale 三個矩陣相乘而來,所以想從 matrix 反推回去幾乎是不太可能。由於我數學太爛,所以我也不知道該怎麼告訴你要怎麼推回去。
你可以照這個畫面把資料輸入進去,這樣就是這個數據所變形出來的結果。
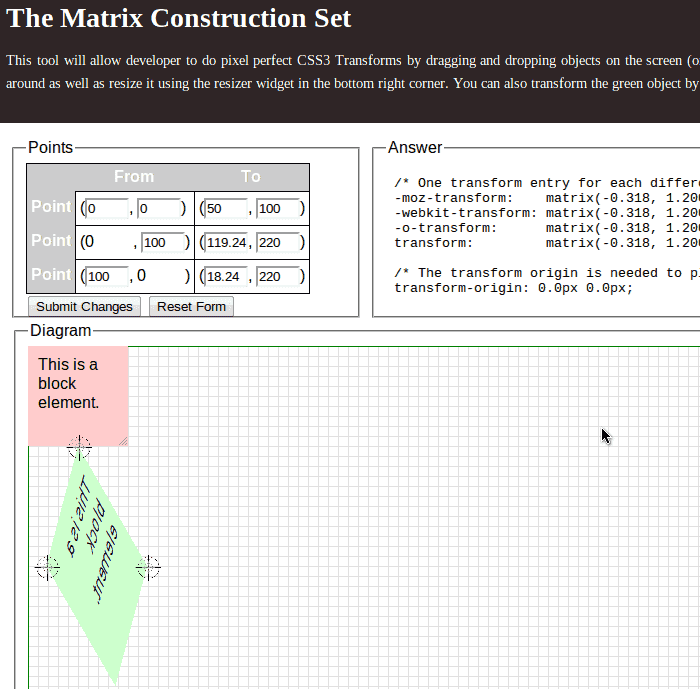
還有一個有趣的地方,假設我們使用 skew,rotate,scale,來去將我們需要的 matrix 算出來的話,倘若直接拿去給瀏覽器,套用到 matrix 中,出來的結果並不一定相同。原因是:Matrix 有其順序性!
Matrix = translate x rotate x scale x skew
依照這種順序所相乘出來的矩陣數值,才是真正 matrix 所表現的樣子。所以在 CSS3 中所要排列的樣子就必須是:
-webkit-transform: translate(50px, 100px) rotate(30deg) scale(1.2) skew(15deg, 30deg);
這樣做出來的效果就等同於使用 matrix 設定:
-webkit-transform: matrix(0.6924, 1.2, -0.3216, 1.2, 50, 100);
不要問我為什麼知道,這種事情作點弊就好了(喂喂喂)。其實也不是作弊,就是是先用矩陣把他乘出來而已。這樣大抵上就是 Transform 在 Matrix 上面的變化了。不過這個東西有個風險,在動態效果頻繁的狀態下,會讓瀏覽器莫名的 Crash 掉,不知道是不是跟我跑在 Ubuntu 底下有關(硬體不太穩定)。
總之,大概就先這樣吧(逃走)。

